Geometry

Meanline models are based on a simplified geometric representation of the turbine, focusing on the parameters defining the flow areas at the inlet, throat, and exit of the cascades, along with several variables necessary for the evaluation of the loss correlations.

Axial Turbine

This section gives a description of the geometry used in simulations of axial turbines. To evaluate the turbine model, the following geometrical variables are required for each cascade:

• Inlet radius at hub, \(r_\mathrm{in, hub}\)

• Inlet radius at tip, \(r_\mathrm{out, tip}\)

• Exit radius at hub, \(r_\mathrm{in, hub}\)

• Exit radius at tip, \(r_\mathrm{out, tip}\)

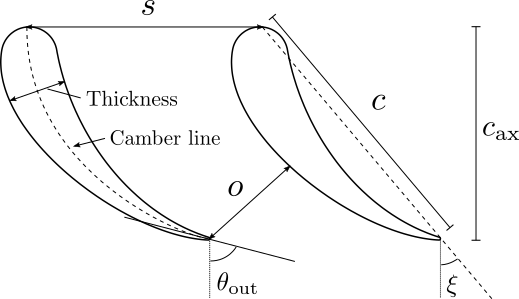
• Pitch, \(s\)

• Chord, \(c\)

• Stagger angle, \(\xi\)

• Opening, \(o\)

• Leading edge metal angle, \(\theta_\mathrm{le}\)

• Leading edge wedge angle, \(We_\mathrm{le}\)

• Leading edge diameter, \(d_\mathrm{le}\)

• Trailing edge thickness, \(t_\mathrm{te}\)

• Maximum blade thickness, \(t_\mathrm{max}\)

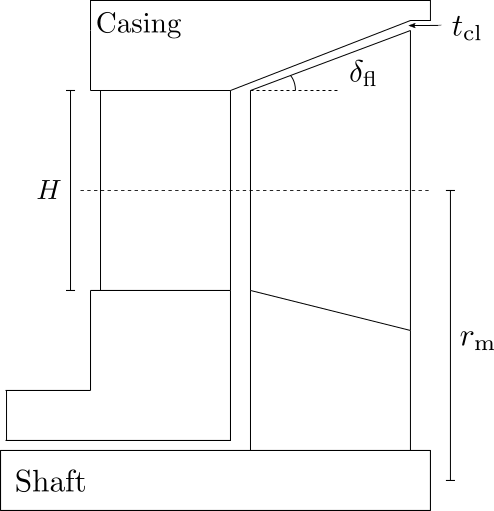
• Tip clearance, \(t_\mathrm{cl}\)

• Throat location factor, \(loc_\mathrm{throat}\)

From this the mean radius at the inlet and exit can be calculated:

\[r_\mathrm{mean} = \frac{r_\mathrm{hub} + r_\mathrm{tip}}{2}\]

And the blade height:

\[H = r_\mathrm{tip} - r_\mathrm{hub}\]

The mean blade height is the mean of the inlet and exit blade height:

\[H_\mathrm{mean} = \frac{H_\mathrm{in} + H_\mathrm{out}}{2}\]

The areas are calculated according to the following function:

\[A = \pi (r_\mathrm{tip}^2 - r_\mathrm{hub}^2)\]

The axial chord is calculated from the stagger angle and chord:

\[c_\mathrm{ax} = c\cos(\xi)\]

The flaring angle is calculated from the blade heights and axial chord:

\[\delta_\mathrm{fl} = \arctan(\frac{H_\mathrm{out} - H_\mathrm{in}}{2c_\mathrm{ax}})\]

The throat radius at hub to tip depend on the flaring and the throat location factor:

\[r_\mathrm{throat} = (1-loc_\mathrm{throat})r_\mathrm{in} + loc_\mathrm{throat}r_\mathrm{out}\]

The blade height at the throat is calculated similarly as for the ither planes and the throat area as

\[A_\mathrm{throat} = 2\pi r_\mathrm{throat, mean} H_\mathrm{throat} \frac{o}{s}\]

The gauging angle is calculated from the throat and exit area:

\[\beta_g = \arccos(\frac{A_\mathrm{throat}}{A_\mathrm{out}})\]

The geometry is illustrated below, both in axial-radial direction (left) and for the cascade profile geometry (right).